Autor serwisu

Jacek Piotr Nowicki
Project Coordinator and programmer
https://jpn.hmcloud.pl

Wprowadzenie do liczb pierwszych

Wiele liczb naturalnych daje się rozłożyć na czynniki mniejsze np. 10=5*2 lub 111=3*37. Jednak istnieją liczby, które nie mogą być rozłożone w taki sposób. Takie liczby nazywamy liczbami pierwszymi.

Liczba pierwsza to taka liczba całkowita p większa od jedności, której jedynymi dziennikami są 1 oraz p. Każdą liczbę naturalną większą od jedności, która nie jest liczbą pierwszą, nazywamy liczbą złożoną.

Liczba 0 z definicji nie jest ani liczbą pierwszą, ani liczbą złożoną.

Liczba 1 z definicji nie jest ani liczbą pierwszą, ani liczbą złożoną.

Pierwsze 34 liczby pierwsze to : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139

Liczb pierwszych jest nieskończenie wiele. Niech π(n) będzie określało ilość liczb pierwszych nie większych od n. Dla dużych wartości liczby n mamy wzór:

Oto kilka przykładów : liczb pierwszych mniejszych od 1000 jest 168. Wśród wszystkich liczb 100-cyfrowych w przybliżeniu jedna na każde 300 jest liczbą pierwszą.

Problem liczb pierwszych polega na ich rozmieszczeniu wśród liczb naturalnych. Nikt nie opracował dotąd żadnego wzoru pozwalającego na wyszukiwanie kolejnych liczb pierwszych. Istnieją wzory wyszukiwania liczb pierwszych o określonych właściwościach, nie ma jednak wzoru, który by dla każdego argumentu generował by liczbę pierwszą.

drukuj

Sito Eratostenesa

Najpopularniejszym algorytmem wyznaczania liczb pierwszych jest Sito Eratostenesa. Oto algorytm :

Ze zbioru liczb naturalnych z przedziału [2,n] wybieramy najmniejszą liczbę 2 i wykreślamy wszystkie jej wielokrotności większe od niej samej.
Z pozostałych liczb wybieramy najmniejszą niewykreśloną liczbę ( jest to liczba 3 ) i usuwamy wszystkie jej wielokrotności większe od niej samej.
Wykreślanie powtarzamy do momentu gdy liczba i, której wielokrotność wykreślamy będzie większa niż pierwiastek z liczby n.
Wszystkie niewykreślone liczby z przedziału [2,n] są liczbami pierwszymi.

drukuj

Gęstość liczb pierwszych

Teraz wprowadzamy nowe pojęcie gęstości liczb pierwszych. Niech A_n oznacza ilość liczb pierwszych wśród liczb naturalnych 1,2,3,...,n. Zatem :

A₁ = 0
A₂ = 1
A₃ = 2
A₄ = 2
A₅ = 3
...

Gęstość liczb pierwszych wśród n pierwszych liczb całkowitych jest dana przez stosunek : A_n / n

Poniżej przedstawiam tabelę zawierającą procent liczb pierwszych w danym przedziale [a,b] :

procent liczb pierwszych z przedziału [a,..,b]

Niech π(n) będzie określało ilość liczb pierwszych nie większych od n. Jak już wspomniałem - dla dużych wartości liczby n mamy wzór:

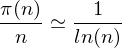
twierdzenie o liczbach pierwszych mówi nam, że :

dąży do 1 przy wzroście liczby n.

drukuj

Rodzaje liczb pierwszych

Liczby Mersenne'a

Niech liczba M_q = 2^q - 1
Niech q będzie liczbą naturalną.

Wtedy M_q jest liczbą Mersenne'a. Sprośród wszystkich wygenerowanych do tej pory liczb tego typu zaledwie 48 to liczby pierwsze.

Liczby pierwsze bliźniacze.

Liczby bliźniacze to dwie liczby pierwsze róźniące się o 2.Na przykład

(3,5)
(5,7)
(59.,61)

Liczby pierwsze czworacze

Liczby czworacze to takie liczby: p , p+2, p+6, p+8, że każda z nich jest liczbą pierwszą.Na przykład

5, 7, 11, 13
821, 823, 827, 829

Liczby pierwsze izolowane

Liczba pierwsza p jest izolowana, jeśli najbliższa liczba pierwsza różni się od niej co najmniej o 4. Na przykład 89, 157, 173.

Liczby Sophie Germain

Liczba pierwsza p jest liczbą Sophie Germain, jeśli liczba 2p+1 także jest liczbą pierwszą.

Liczby pierwsze lustrzane

To pary liczb pierwszych, z których jedna powstaje przez zapisanie cyfr dziesiętnych drugiej w odwrotnej kolejności. Przykłady:

13 i 31
17 i 71

Liczby pierwsze palindromiczne

To liczby pierwsze, które nie zmieniają się, gdy ich cyfry dziesiętne zapiszemy w odwrotnej kolejności. Przykłady: 11, 101, 131, 191, 929.

drukuj

Wzory na liczby pierwsze

Próbowano znaleźć proste wzory arytmetyczne, które dawałyby tylko liczby pierwsze, chociaż niekoniecznie wszystkie liczby pierwsze. Fermat wysunął słynne przypuszczenie, że wszystkie liczby postaci :

F(n) = 2^2ⁿ + 1

są liczbami pierwszymi. Rzeczywiści dla n=1,2,3,4 otrzymujemy :

F(1)=5
F(2)=7
F(3)=257
F(4)=65537

Wszystkie powyższe liczby są pierwsze. Ale w roku 1723 Euler odkrył, że F(5)=641*6700417 nie jest liczbą pierwszą.

Innym ciekawym wyrażeniem, które daje wiele liczb pierwszych jest

F(n) = n² - n + 41

Dla n=1,2,3,...,40 wyrażenie f(n) jest liczbą pierwszą. Natomiast dla n=41 mamy f(n)=412 i jest to liczba złożona.

Wyrażenie

F(n) = n² - 79n + 1601

daje liczby pierwsze przy wszelkich wartościach n aż do 79. Zawodzi jednak dla n=80

drukuj

Testy pierwszości

Aby sprawdzić, czy liczba naturalna n jest liczbą pierwszą, należy dzielić ją kolejno przez wszystkie liczby większe od 1 i mniejsze równe od floor(n/2). Jeśli przy każdym dzieleniu reszta z dzielenia jest różna od zera, to liczba jest liczbą pierwszą. Natomiast jeżeli choć jedno dzielenie daje resztę równą zero, to sprawdzana liczba naturalna jest liczbą złożoną.

Oto przykład funkcji sprawdzającej czy dana liczba n jest liczbą pierwszą. Funkcja została napisana w języku PHP

Jeżeli funkcja zwróci wartość 0 to liczba n jest liczbą pierwszą.

drukuj

Spirala Ulama

W matematyce spirala Ulama lub spirala liczb pierwszych to graficzna metoda pokazywania pewnych niewyjaśnionych do dziś różnic w rozkładzie liczb pierwszych, zaproponowana przez polskiego matematyka Stanisława Ulama w 1963 roku. Na kwadratowej tablicy zaczynając od 1 w środku spiralnie wypisuje się kolejne liczby naturalne. Na niektórych przekątnych liczby pierwsze częściej grupują się niż na innych. Fakt ten nie został do tej pory wyjaśniony.

Liczby od 1 do 50 w układzie spirali Ulama

Liczby pierwsze w tym samym układzie

Liczby pierwsze w Spirali Ulama w układzie 200x200

Hipotezy

Czego nie wiadomo o liczbach pierwszych:

Hipoteza 1
Czy istnieje liczba pierwsza między n² a (n+1)² dla każdego n>0?

Hipoteza 2
Czy istnieje nieskończenie wiele liczb pierwszych postaci n²+1 gdzie n jest liczbą całkowitą?

Hipoteza 3
Czy każda liczba parzysta jest sumą dwóch nieparzystych liczb pierwszych?

Hipoteza 4
Czy istnieje nieskończenie wiele par liczb pierwszych, takich jak 11,13 albo 17,19 różniących się o 2. Jest to problem bliźniaczych liczb pierwszych.

drukuj

Ciekawostki

Ciekawostka 1
W 1914 roku amerykański matematyk Derrick Norman Lehmer opublikował po raz pierwszy listę wszystkich 664579 liczb pierwszych mniejszych od 10 milionów. Stworzył on tę listę za pomocą sita Eratostenesa.

Ciekawostka 2
Liczba 11111111111111111111111 złożona z 23 jedynek jest liczbą pierwszą.

Ciekawostka 3
Liczba 31415926535897932384626433832795028841 zestawiona z początkowych 38 cyfr rozwinięcia dziesiętnego liczby π , jest liczbą pierwszą.

Ciekawostka 4
Liczba 73939133 nie tylko jest liczbą pierwszą, ale liczby otrzymane z niej przez kolejne obcinanie cyfr od prawej strony też są liczbami pierwszymi:

7393913 jest liczbą pierwszą
739391 jest liczbą pierwszą
73939 jest liczbą pierwszą
7393 jest liczbą pierwszą
739 jest liczbą pierwszą
73 jest liczbą pierwszą
7 jest liczbą pierwszą

drukuj

Największe liczby pierwsze

Największa odkryta dotąd liczba pierwsza to 2^74207281−1, która liczy sobie 22338618 cyfr w zapisie dziesiętnym. Została ona odkryta przez Curtisa Coopera 7 stycznia 2016 roku.

Oto lista innych wielkich liczb pierwszych:

Największą liczbą pierwszą sprzed ery komputerów jest liczba, która nosi nazwę odkrywcy - liczba Ferriera i wynosi:

20 988 936 657 440 586 486 151 264 256 610 222 593 863 921

Jest to 44-cyfrowa liczba znaleziona za pomocą mechanicznego kalkulatora w 1951r.

drukuj

Kryptografia

Duże liczby pierwsze są często wykorzystywane w kryptografii ze względu na swe specyficzne właściwości. Dla przykładu opiszę kryptosystem RSA. Wykorzystujemy tutaj dwie pary kluczy : klucz publiczny i klucz prywatny

1. Najpierw generujemy klucz publiczny oraz klucz prywatny:

wybieramy losowo dwie liczby pierwsze p i q.
obliczamy iloczyn tych liczb n=pq
obliczamy wartość funkcji Eulera dla n : φ(n)=(p-1)(q-1)
wybieramy liczbę e z przedziału [1,n] względnie pierwszą z φ(n)
znajdujemy liczbę d : d=e^-1 mod φ(n)
klucz publiczny to para liczb (n,e)
klucz prywatny to para liczb (n,d)

2. Szyfrowanie i deszyfrowanie

Aby zaszyfrować wiadomość dzielimy ją na bloki mi o wartości nie większej niż n
Teraz każdy z bloków szyfrujemy według wzoru : c_i = m_i^e mod n
Natomiast aby odszyfrować wiadomość musimy każdy z bloków c_i odszyfrować według wzoru : m_i = c_i^d mod n

drukuj

Algorytmy probabilistyczne

Algorytmy probabilistyczne z bardzo dużym prawdopodobieństwem sprawdzają czy dana liczba jest liczbą pierwszą. Ale niestety istnieje niewielkie prawdopodobieństwo pomyłki.

Algorytm:

Wprowadź liczbę n
Wybierz losowo liczbę k z przedziału [1,n-1]
Sprawdź czy liczba k świadczy o złożoności liczby n
1. Jeżeli tak to liczba n nie jest liczbą pierwszą
2. Jeżeli nie to sprawdź czy sprawdzono już 200 różnych liczb k
  1. Jeżeli nie to wróć do punktu 2
  2. Jeżeli tak to n jest liczbą pierwszą.

drukuj

W powyższym algorytmie prawdopodobieństwo pomyłki jest mniejsze niż 1/200.

Funkcja Eulera

Dla każdego n>=1 niech φ(n) będzie liczbą takich liczb całkowitych z przedziału 1<=a<=n, że NWD(a,n)=1. Wtedy funkcję φ nazywamy funkcją Eulera.

Własność 1
Nich p będzie liczbą pierwszą. Wtedy φ(p)=p-1

Własność 2
Niech m>=1 oraz n>=1 oraz NWD(m,n)=1. Wtedy φ(mn)=φ(m)φ(n).

Własność 3
Niech p będzie liczbą pierwszą. Wtedy φ(p^k)=p^k-1(p-1)

Małe twierdzenie Fermata
Jeżeli p jest liczbą pierwszą, nie będącą dzielnikiem liczby całkowitej a to :

a^φ(p) ≡ 1 (mod p)

Oto przykład algorytmu wyliczającego funkcję Eulera w języku PHP. Użyłem funkcji pomocniczej nwd, która oblicza największy wspólny dzielnik dla dwóch liczb naturalnych większych od 0.

W poniższej tabeli podałem wartości funkcji Eulera dla kolejnych potęg liczby 10.

Wartość funkcji Eulera dla kolejnych potęg liczby 10

drukuj

Książki o liczbach pierwszych

Paulo Ribenboim, Mała księga wielkich liczb pierwszych, Wydawnictwo Naukowo-Techniczne, Warszawa 1997.
Andrzej Szepietowski, Matematyka Dyskretna, Wydawnictwo Uniwersytetu Gdańskiego, Gdańsk 2000.
Wacław Marzantowicz, Piotr Zarzycki, Elementy Teorii Liczb, Wydawnictwo Naukowe UAM
Piotr Zarzycki, Elementarna teoria liczb, PWN, Warszawa 2006.
R. Courant, H. Robbins, Co to jest Matematyka, Państwowe Wydawnictwo Naukowe, Warszawa 1959
Wacław Sierpiński, Arytmetyka Teoretyczna, Państwowe Wydawnictwo Naukowe, Warszawa 1968
Philip J. Davis, Reuben Hersh, Świat Matematyki, Wydawnictwo Naukowe PWN, Warszawa 1994
I.N. Bronsztejn, K.A. Siemiendiajew, G. Musiol, H. Muhlig, Nowoczesne Kompendium Matematyki, Wydawnictwo Naukowe PWN, Warszawa 2007
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Wprowadzenie do algorytmów, Wydawnictwa Naukowo-Techniczne, Warszawa 1998
Marcin Karbowski, Podstawy Kryptografii, Wydawnictwa Helion, Gliwice 2014
David Harel, Yishai Feldman, Rzecz o istocie informatyki - Algorytmika, Wydawnictwa Naukowo-Techniczne, Warszawa 2008
Jacek Wojdanowski, Kod liczb pierwszych, Wydawnictwo Poligraf, Brzezia Łąka 2016
Lubina Jan, Zagadka wszechczasów - rozwiązana , Wydawnictwo Poligraf, Brzezia Łąka 2017
Michał Zalewski, Cisza w sieci, Wydawnictwo Helion 2005

Ciekawe filmy o liczbach pierwszych

film zapożyczony z serwisu Pasja Informatyki

film zapożyczony z serwisu Khan Academy

Ciekawe linki do stron o liczbach pierwszych

Inne rzeczy

Lista liczb pierwszych od 2 do 1000000 w formacie PDF : zobacz
Baza danych liczb pierwszych z przedziału [2,10000] w formacie SQL : zobacz